PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI
W KLASACH I-III ZASADNICZEJ SZKOŁY ZAWODOWEJ
Oczekiwane osiągnięcia uczniów w wyniku realizacji programu nauczania to wymagania programowe. Oceny są w skali 1-6, dlatego przyjęto sześciostopniowy układ wymagań.
Wydzielone zostały następujące wymagania programowe:
- Wymagania konieczne (K) dotyczą zagadnień elementarnych, stanowiących swego rodzaju podstawę, zatem powinny być opanowane przez każdego ucznia.
- Wymagania podstawowe (P) zawierają wymagania z poziomu (K), wzbogacone
o typowe problemy o niewielkim stopniu trudności.
- Wymagania rozszerzające (R), zawierające wymagania z poziomów (K) i (P), dotyczą zagadnień bardziej złożonych i nieco trudniejszych.
- Wymagania dopełniające (D), zawierające wymagania z poziomów (K), (P) i (R), dotyczą zagadnień problemowych, trudniejszych, wymagających umiejętności przetwarzania przyswojonych informacji.
- Wymagania wykraczające (W) dotyczą zagadnień trudnych, oryginalnych, wykraczających poza obowiązkowy program nauczania.
Poniżej przedstawiony został podział wymagań na poszczególne oceny szkolne:
ocena dopuszczająca (2) – wymagania na poziomie (K),
ocena dostateczna (3) – wymagania na poziomie (K) i (P),
ocena dobra (4) – wymagania na poziomie (K), (P) i (R),
ocena bardzo dobra (5) – wymagania na poziomie (K), (P), (R) i (D),
ocena celująca (6) – wymagania na poziomie (K), (P), (R), (D) i (W).
Połączenie wymagań koniecznych i podstawowych a także rozszerzających
i dopełniających pozwoli nauczycielowi dostosować wymagania do specyfiki klasy.
Wymagania na ocenę celującą obejmują dodatkowo materiał rozszerzony, objęty programem.
Ponadto ocenę celującą otrzymuje uczeń, który:
- samodzielnie i twórczo rozwija własne uzdolnienia,
- biegle posługuje się zdobytymi wiadomościami w rozwiązywaniu problemów teoretycznych lub praktycznych z programu nauczania danej klasy,
- proponuje rozwiązania nietypowe,
- rozwiązuje także zadania wykraczające poza program nauczania danej klasy,
- bierze udział i osiąga sukcesy w konkursach przedmiotowych.
Ocenę niedostateczną otrzymuje uczeń, który nie spełnia wymagań na ocenę dopuszczającą.
- Praktyczne zastosowanie statystyki
Stopień |
Wymagania |
Dopuszczający (2)
|
Uczeń potrafi:
- wymienić podstawowe pojęcia statystyczne i podać ich przykłady,
- przedstawić dane za pomocą wykresu słupkowego (pojedynczą serię),
- odczytywać na podstawie wykresu słupkowego, ile obiektów posiada daną cechę, która cecha występuje najczęściej, a która występuje najrzadziej,
- obliczać średnią arytmetyczną dla danych w postaci szeregu indywidualnego, np.: Tomek otrzymał następujące oceny końcowe:
2, 3, 5, 4 ,3 ,4 ,4 ,3, 4, 3 ,5, 4
Oblicz średnią arytmetyczną ocen Tomka? |
Dostateczny (3)
|
Uczeń potrafi:
- podać przykłady badań statystycznych; dla podanego badania określać zbiorowość i jednostkę statystyczną oraz badane cechy,
- przedstawić dane za pomocą wykresu słupkowego (dwie lub więcej serii),
- porównywać na podstawie wykresu słupkowego dwie zbiorowości,
- omawiać na podstawie wykresu liniowego rozwój zjawiska w czasie,
- obliczać średnią arytmetyczną dla danych przedstawionych w postaci szeregu rozdzielczego,
- obliczać modalną dla danych przedstawionych w postaci szeregu indywidualnego i rozdzielczego bez przedziałów.
|
Dobry (4) |
Uczeń potrafi:
- przedstawić strukturę zbiorowości przy pomocy wykresu kołowego,
- przedstawić serie danych statystycznych w postaci wykresu liniowego,
- mając podaną liczebność całej zbiorowości, na podstawie wykresu kołowego wyliczać, ile obiektów posiada daną cechę, np.:
Na obóz językowy do Paryża przyjechało 150 osób z pięciu krajów. Na podstawie wykresu odpowiedz na pytania:
- Ilu Polaków przyjechało na obóz?
- Ile osób przyjechało z europy Południowej?
-O ile osób mniej przyjechało z Niemiec niż z Holandii?
- na podstawie wykresu obliczać średnią arytmetyczną przedstawionych danych,
- obliczać medianę dla danych przedstawionych w postaci szeregu indywidualnego.
|
Bardzo dobry (5) |
Uczeń potrafi:
- przygotowywać i przeprowadzać badanie ankietowe oraz prezentować wyniki tego badania w postaci różnego rodzaju wykresów statystycznych,
- obliczać średnią arytmetyczną dla danych przedstawionych w postaci szeregu rozdzielczego z przedziałami,
- porównywać dla danych przedstawionych w postaci szeregu indywidualnego wielkość średniej arytmetycznej, modalnej i mediany.
|
Stopień |
Wymagania |
Dopuszczający (2) |
Uczeń potrafi:
- rozpoznawać funkcje kwadratowe i podawać wzorem przykłady takich funkcji,
- szkicować wykres funkcji y=ax2 dla a? 0,
- odczytywać wartości współczynników a, b, c z postaci ogólnej funkcji kwadratowej,
- określać, w zależności od znaku wyróżnika, ile miejsc zerowych ma funkcja kwadratowa,
- obliczać miejsca zerowe funkcji kwadratowej danej w postaci iloczynowej lub ogólnej,
- sprawdzać, czy dana liczba jest pierwiastkiem równania kwadratowego,
- określać, w zależności od znaku wyróżnika, ile pierwiastków ma równanie kwadratowe.
|
Dostateczny (3) |
Uczeń potrafi:
- szkicować wykres funkcji kwadratowej określonej w postaci kanonicznej,
- zapisywać w postaci ogólnej funkcję kwadratową daną w postaci kanonicznej,
- wyznaczać współrzędne wierzchołka oraz współrzędne punktów przecięcia z osiami układu współrzędnych i na tej podstawie szkicować wykres funkcji kwadratowej,
- zapisywać trójmian kwadratowy w postaci kanonicznej,
- zapisywać trójmian w postaci iloczynowej,
- rozwiązywać równania kwadratowe zupełne i niezupełne o współczynnikach całkowitych.
|
Dobry (4) |
Uczeń potrafi:
- odczytywać podstawowe własności funkcji kwadratowej na podstawie jej wykresu (zbiór wartości, monotoniczność, wartości dodatnie, wartości ujemne),
- rozwiązywać równania kwadratowe o współczynnikach całkowitych, np.: 5x + 4 +x2 = 0, 2 - 4x – 2x2 =0
- rozwiązywać zadania tekstowe prowadzące do równań kwadratowych, np.: kwadrat sumy dwóch kolejnych liczb naturalnych wynosi 529. Co to za liczby?
- stosować wzory Viete'a do obliczania pierwiastków równania kwadratowego w pamięci,
- obliczać wartości wyrażeń typu (x1 + x2)2, gdzie x1 i x2 są pierwiastkami równania kwadratowego ax2 + bx + c = 0, a?0
- rozwiązywać nierówności kwadratowe, np.:
9x2 – 12x + 4< 0,
3x2 + 27> 0 |
Bardzo dobry (5) |
Uczeń potrafi:
- zapisać wzór funkcji kwadratowej, której wykres można otrzymać w wyniku przesunięcia równoległego wykresu funkcji y = ax2 ,
- stosować własności funkcji kwadratowej do rozwiązywania zadań tekstowych, np.:
Liczbę 20 przedstaw jako sumę takich dwóch liczb, aby ich iloczyn był największy.
- rozwiązać równanie kwadratowe o podwyższonym stopniu trudności, np.:
2(x – 1)2 = 2x – x2 , (1 – x)(1 + x) = x2 + 2x
- rozwiązywać zadania tekstowe prowadzące do równania kwadratowego, np.: Bawiły się raz małpy – wieść indyjska niesie
Ósma ich część w kwadracie już skacze po lesie.
Pozostałych dwanaście w pląsach i z wrzaskami
Pomiędzy zielonymi hasa pagórkami.
Ile ich wszystkich było? Pyta Bhaskara.
Zagadka nie jest trudna, chociaż bardzo stara.
- obliczać wartości wyrażeń typu
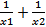 , gdzie x1 i x2 są pierwiastkami równania kwadratowego ax2 + bx + c = 0, a ? 0 , gdzie x1 i x2 są pierwiastkami równania kwadratowego ax2 + bx + c = 0, a ? 0
- rozwiązywać nierówności kwadratowe o podwyższonym stopniu trudności, np.: (x – 2)(2x + 3) + 11 ? 0
2(x – 3)(x + 1) ? -6 |
Stopień |
Wymagania |
Dopuszczający (2) |
Uczeń potrafi:
- porządkować wielomiany,
- określać stopień wielomianu,
- obliczać wartość wielomianu dla podanej wartości zmiennej,
- obliczać sumę i różnicę dwóch wielomianów,
- sprawdzać, która z podanych liczb jest pierwiastkiem wielomianu,
- wyznaczać pierwiastki wielomianu danego w postaci iloczynu czynników stopnia pierwszego,
- określać krotność pierwiastka wielomianu danego w postaci iloczynowej.
|
Dostateczny (3) |
Uczeń potrafi:
- obliczać iloczyn wielomianu przez jednomian,
- obliczyć iloczyn wielomianu przez dwumian,
- dzielić wielomianu przez jednomian,
- wyznaczyć pierwiastki wielomianu danego w postaci iloczynu dwumianu liniowego i trójmianu kwadratowego,
- wyznaczyć pierwiastki wielomianu danego w postaci iloczynu czynników stopnia drugiego,
- rozkładać wielomiany na czynniki poprzez wyłączanie wspólnego czynnika przed nawias.
|
Dobry (4) |
Uczeń potrafi:
- dzielić wielomian przez dwumian,
- bez wykonywania dzielenia sprawdzić, czy wielomian jest podzielny przez dwumian,
- bez wykonywania dzielenia obliczać resztę z dzielenia wielomianu przez dwumian,
- rozkładać wielomian na czynniki metodą grupowania wyrazów,
- rozkładać wielomian na czynniki, stosując wzory skróconego mnożenia,
- wyznaczać pierwiastki wielomianu danego w postaci iloczynowej, np.:
W(x) = x5(6x – 12)3(14x + 7)2
W(x) = 4(x -4)2 (x +?3)(x + 5)3
- rozwiązywać równania stopnia trzeciego, np.: x3 + 7x2 + x + 7 = 0
x3 – 2x2 – x + 2 = 0
rozkładać wielomiany na czynniki dane w postaci iloczynu czynników stopnia drugiego, np.: (x2 – 25)(x2 – 4x + 4)
- rozkładać wielomiany na czynniki, np.: M(x) = 3x3 – 2x2 –x
P(x) = x4 – 4x2 |
Bardzo dobry (5) |
Uczeń potrafi:
- mając jeden pierwiastek wielomianu, obliczyć pozostałe,
- wyznaczyć pierwiastki wielomianu, np.: T(x) = x3 – 9x
T(x) = 4x3 – x2 – 4x +1
- rozkładać wielomian na czynniki, znając jeden z jego pierwiastków,
- rozwiązywać równania stopnia trzeciego, np.: 4x3 – 2x2 + 6x – 3 = 0
- rozwiązywać równanie stopnia trzeciego, znając jeden jego pierwiastek,
- rozwiązywać nierówności stopnia trzeciego.
|
Stopień |
Wymagania |
Dopuszczający (2) |
Uczeń potrafi:
- określać wzajemne położenie prostych i płaszczyzn w przestrzeni,
- podawać przykłady prostych i płaszczyzn w przestrzeni,
- rozpoznawać wielościany i nazywać je,
- rozpoznawać figury obrotowe i omawiać sposoby ich powstawania,
- rysować modele graniastosłupów, ostrosłupów, walców, stożków i kul,
- wymieniać podstawowe jednostki objętości,
- obliczać pole i objętość sześcianu i prostopadłościanu, mając dane potrzebne wielkości,
- obliczać pole i objętość kuli, gdy dany jest promień.
|
Dostateczny (3) |
Uczeń potrafi:
- wskazywać kąt miedzy prostą i płaszczyzną,
- stosować twierdzenie Pitagorasa do wyznaczania nieznanych wielkości w ostrosłupie i stożku,
- rysować siatki brył,
- obliczać pola i objętości graniastosłupów prostych, gdy dane są potrzebne wielkości,
- obliczać pola i objętości ostrosłupów prawidłowych, gdy dane są potrzebne wielkości,
- obliczać pole i objętość walca i stożka, gdy dane są potrzebne wielkości,
- obliczać długość krawędzi sześcianu, gdy dane jest jego pole lub objętość,
- obliczać długość promienia kuli, gdy dane jest jej pole lub objętość ( w prostych przykładach),
- rysować przekrój osiowy bryły obrotowej.
|
Dobry (4) |
Uczeń potrafi:
- wskazywać i zaznaczać kąty w ostrosłupach,
- obliczać miarę kąta dwuściennego, np.:
W ostrosłupie prawidłowym czworokątnym dane są: krawędź podstawy 8 cm i wysokość ściany bocznej 5 cm. Oblicz kąt nachylenia ściany bocznej do płaszczyzny podstawy.
- stosować funkcje trygonometryczne do wyznaczania nieznanych wielkości w ostrosłupie i stożku, np.:
Tworząca stożka ma dl. 12 cm i tworzy z płaszczyzną podstawy kąt o mierze 300. Oblicz:
- długość promienia stożka
- wysokość stożka
- pole powierzchni całkowitej i objętość tego stożka.
- wykorzystywać pojęcie przekroju osiowego bryły obrotowej do rozwiązywania zadań, np.:
Przekrój osiowy stożka jest trójkątem o polu 72cm2 i kącie przy podstawie 450 .
Oblicz pole powierzchni całkowitej i objętość tego stożka.
- przeliczać jednostki objętości,
- obliczać objętość kuli, gdy dane jest pole powierzchni i odwrotnie,
- stosować zdobytą wiedzę do rozwiązywania problemów z życia codziennego, np.:
Wysokość beczki w kształcie walca wynosi 60cm, a średnica jej podstawy ma długość 40 cm. Oblicz pojemność tej beczki w litrach. |
Bardzo dobry (5) |
Uczeń potrafi:
- stosować własności wielościanów do rozwiązywania zadań trudniejszych, np.:
Oblicz pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, którego pole podstawy wynosi 36 cm2 , a kąt miedzy przekątną ściany bocznej i krawędzią podstawy ma miarę 300 .
- stosować własności figur obrotowych do rozwiązywania zadań trudniejszych, np.:
- Obwód podstawy walca jest równy 20? cm. Przekątna przekroju osiowego tworzy z podstawą kąt 300 . Oblicz wysokość tego walca.
- Przekrój osiowy kuli jest kołem o polu równym 121? cm2 . Oblicz pole powierzchni i objętość tej kuli.
- stosować pojęcie gęstości substancji do rozwiązywania zadań dotyczących problemów z życia codziennego, np.:
Wróżka zamówiła szklaną kulę o średnicy 18 cm. Oblicz wagę tej kuli, jeżeli gęstość szkła wynosi 2,5g/cm3 .
- stosować zdobytą wiedzę do rozwiązywania nietypowych problemów z życia codziennego, np.:
- Basen w kształcie prostopadłościanu ma wymiary: długość 25 m, szerokość
15 cm. Głębokość wody w basenie wynosi 2m. Oblicz, po jakim czasie woda w basenie zostanie przefiltrowana w całości, jeżeli filtr działa z wydajnością
50 m3 / godz.
- Średnica obranej ze skórki pomarańczy ma 6 cm, a wyciśnięty z pomarańczy sok stanowi 75% jej objętości. Porcja soku 300ml kosztuje 3,50zł. Oblicz ile pomarańczy potrzeba na jedną porcję soku i ile zapłacimy za sok z czterech pomarańczy. |
W klasie II ZSZ ( dwuletniej) program nauczania jest realizowany w całości, natomiast w klasie
II ZSZ ( trzyletniej) wielomiany są przeniesione do klasy III ZSZ oraz większość stereometrii ( 63%) jest również realizowana w III klasie ZSZ
WYMAGANIA DLA KLASY PIERWSZEJ ZASADNICZEJ SZKOŁY ZAWODOWEJ
Stopień |
Wymagania |
Dopuszczający (2)
|
Uczeń potrafi:
- podać przykłady zbiorów
- wymienić elementy danego zbioru
- rozpoznać i zbudować proste zdanie logicznie prawdziwe i fałszywe
- rozpoznawać liczby naturalne, całkowite, wymierne i niewymierne oraz podawać ich przykłady
- wymienić elementy sumy, części wspólnej i różnicy zbiorów
- porównać dwie dowolne liczby wymierne
- wykonać podstawowe działania na liczbach wymiernych z uwzględnieniem zamiany ułamka zwykłego na dziesiętny i odwrotnie
- wykonywać działania pisemne na liczbach naturalnych
- dodawać, odejmować, mnożyć i dzielić ułamki dziesiętne i zwykłe
- obliczać wartość liczbową wyrażeń dla podanych wartości zmiennych w prostych przykładach np.: 7a2 – 4ab +6b – 20 dla a = -3 i b= 2
- obliczyć procent danej liczby
- obliczyć wartość prostych wyrażeń arytmetycznych zawierających potęgi o wykładnikach naturalnych i pierwiastki
- obliczyć wartość potęgi o wykładniku naturalnym
- przedstawić daną liczbę wymierną i dane przedziały na osi liczbowej
- obliczyć wartość bezwzględną liczby rzeczywistej
- przekształcić proste wyrażenie algebraiczne
- sprawdzić, czy dana liczba jest rozwiązaniem równania, nierówności I pierwszego stopnia z jedną niewiadomą
- rozwiązać równanie i nierówność pierwszego stopnia z jedną niewiadomą
- ułożyć równanie do zależności przedstawionej tekstem
|
Dostateczny (3)
|
Uczeń potrafi:
- wyznaczyć sumę, iloczyn i różnicę dwóch danych zbiorów
- rozpoznać i zbudować: negację, alternatywę, koniunkcję, implikację, równoważność zdań
- wyznaczyć przybliżenie danej liczby z zadaną dokładnością
- potęgować liczby wymierne (potęgą o wykładniku całkowitym)
- znajdować przybliżenie dziesiętne liczb wymiernych
- rozwiązać proste zadanie tekstowe prowadzące do obliczeń:
- procentu danej liczby
- liczby na podstawie danego jej procentu
- jakim procentem jednej liczby jest druga liczba
- obliczyć średnią arytmetyczną danych liczb
- obliczyć wartość potęgi o wykładniku wymiernym
- rozkładać wyrażenia algebraiczne na czynniki poprzez wyłączanie wspólnego czynnika przed nawias, np.: 7a4 – 6a2b +5a2
- suwać niewymierności w wyrażeniu:
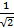
- rozstrzygnąć czy dana liczba należy do danego przedziału liczbowego
- obliczyć wartość liczbową wyrażenia algebraicznego z wykorzystaniem wzorów skróconego mnożenia w prostych o przykładach, np.: (3a – 2)2
- rozwiązać proste równanie i nierówność
|
Dobry (4)
Dobry (4) |
Uczeń potrafi:
- wykonać działania na przedziałach liczbowych
- wykonać działania na liczbach rzeczywistych, stosując prawa działań
- stosować w praktyce obliczenia procentowe,
- obliczać medianę ciągu liczb
- wyłączyć czynnik pod znak pierwiastka i wyłączyć czynniki spod znaku pierwiastka
- porównywać pierwiastki
- usuwać niewymierność z mianownika, np.:
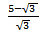
- wykonywać działania w zbiorze liczb wymiernych, wykorzystując kolejność działań
- rozwiązać równanie, nierówność, nierówność podwójną
- rozwiązać zadanie tekstowe o złożonych zależnościach prowadzące do rozwiązania równania lub nierówności liniowej
- rozwiązać zadanie tekstowe wykorzystując obliczenia procentowe
- stosować wzory skróconego mnożenia do upraszczania wyrażeń algebraicznych, do rozkładu wyrażeń algebraicznych na czynniki
- stosować średnią arytmetyczną do rozwiązywania zadań praktycznych
|
Bardzo dobry (5) |
Uczeń potrafi:
- stosować własności działań na zbiorach
- oceniać wartość logiczną negacji, alternatywy, koniunkcji, implikacji, równoważności zdań
- obliczyć błąd bezwzględny i względny przybliżenia, szacować wartości liczbowe
- konstruować odcinek o długości
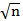 n € N n € N
- wykonywać trudniejsze działania na liczbach wymiernych
- stosować własności działań na potęgach i pierwiastkach
- usuwać niewymierność z mianownika
- rozkładać na czynniki, wykorzystując metodę grupowania
- przekształcać wzory z różnych dyscyplin nauki
- rozwiązywać zdania tekstowe prowadzące do równania z wykorzystaniem obliczeń procentowych, wzór na kapitalizację odsetek
- matematyzować problemy z życia codziennego
|
Stopień |
Wymagania |
Dopuszczający (2)
Dopuszczający (2)
|
Uczeń potrafi:
- rozstrzygnąć, czy przyporządkowanie zadane grafem, wykresem lub tabelą jest funkcją
- określać funkcje za pomocą: grafu, tabeli, wzoru, wykresu, opisu słownego
- obliczyć wartość funkcji liczbowej danej wzorem
- wskazać zbiór argumentów funkcji zdanej grafem, tabelką lub wykresem
- zaznaczyć punkty o danych współrzędnych i odczytać współrzędne danego punktu w prostokątnym układzie współrzędnych
- wykonać wykres prostych zależności funkcyjnych opisanych słownie, tabelką, wzorem ( rysować wykres funkcji liniowej)
- odczytać wartość funkcji dla danego argumentu na podstawie jej wykresu funkcji lub tabeli
- odczytać argument funkcji dla danej jej wartości z wykresu funkcji lub tabeli
- odczytać miejsca zerowe z wykresu funkcji
- określić monotoniczność funkcji na podstawie prostych wykresów funkcji ciągłych
- wykonać wykres funkcji f(x) = ax + b, gdzie a€ W i b € W
- odczytać własności funkcji liniowej ( dziedzina, zbiór wartości, miejsce zerowe, monotoniczność, znaki) na podstawie wykresu
- obliczyć współrzędne punktów przecięcia z osiami układu współrzędnych wykresu funkcji liniowej
- rozpoznać wielkości wprost proporcjonalne oraz sporządzić wykres tej zależności
- podać przykład równania liniowego z dwiema niewiadomymi
- podać przykłady rozwiązań równania liniowego z dwiema niewiadomymi
- rozwiązać proste nierówności liniowe i układy równań stopnia pierwszego z dwiema niewiadomymi
- sprawdzić, czy dana para liczb jest rozwiązaniem układu równań liniowych
- rozwiązać prosty układ równań liniowych wybraną przez siebie metodą algebraiczną
|
Dostateczny (3)
|
Uczeń potrafi:
- wskazać zależność funkcyjną w różnych sytuacjach np. zależność fizyczną, geometryczną
- wskazać zbiór wartości funkcji na podstawie wykresu lub tabelki
- obliczyć argument funkcji liniowej, gdy dana jest wartość funkcji
- obliczyć miejsca zerowe funkcji liniowej
- wykonać wykres funkcji liniowej danej w postaci ogólnej
- odczytać z wykresu podstawowe własności funkcji
- przesuwać wykres wzdłuż osi X lub osi Y
- wyznaczyć dziedzinę funkcji określonej prostym wzorem
- wyznaczyć wzór funkcji liniowej, gdy dane są współrzędne punktu należącego do wykresu i współczynnik kierunkowy funkcji
- omówić wszystkie własności funkcji liniowej
- badać własności funkcji określanych tym samym wzorem, ale na różnych dziedzinach
- wyznaczyć dziedzinę funkcji liczbowej na podstawie wzoru
- przedstawić zbiór rozwiązań równania liniowego z dwiema zmiennymi w układzie współrzędnych
- rozwiązać równanie liniowe i nierówności liniowe o średnim stopniu trudności
- podać przykłady rozwiązań danej nierówności
- rozpoznać typy układów równań liniowych na podstawie ich graficznej ilustracji
- rozwiązać układy równań liniowych metodami podstawiania lub/ i przeciwnych współczynników oraz graficznie
- rozwiązać za pomocą układu równań proste zadanie tekstowe np.:
- Suma trzech liczb nieparzystych wynosi 87. Wyznacz te liczby
- za dwie książki Tomek zapłacił 60zł. Jedna z książek jest o 40% droższa od drugiej. Ile kosztowała każda książka? |
Dobry (4) |
Uczeń potrafi:
- badać monotoniczność funkcji z wykorzystaniem definicji
- rozwiązywać zadania tekstowe prowadzące do równań liniowych, np.:
- Na lekcji matematyki 15% uczniów nie rozwiązała zadania, 30% rozwiązało z błędami, a pozostałych 11 uczniów rozwiązało zadanie poprawnie. Ilu uczniów liczyła klasa?
- rozwiązać graficznie układ nierówności liniowych z dwiema niewiadomymi
- rozwiązać zadanie tekstowe prowadzące do układu nierówności liniowych, np.:
-Ile krzeseł ogrodowych w cenie 29,89 zł można kupić, mając do dyspozycji 500 zł?
- rozwiązywać nierówności liniowe o średnim stopniu trudności
- rozwiązywać układy dwóch równań stopnia pierwszego z dwiema niewiadomymi
- podawać interpretację geometryczną układu dwóch równań stopnia pierwszego z dwiema niewiadomymi
- rozwiązywać zadania tekstowe prowadzące do układów dwóch równań stopnia pierwszego z dwiema niewiadomymi, np.:
- Za 30 biletów do kina zapłacono 440 zł. Bilety dla dorosłych były po 20 zł, a dla
dzieci – o40% tańsze. Ile kupiono biletów dla dorosłych, a ile dla dzieci? |
Bardzo dobry (5) |
Uczeń potrafi:
- przesunąć wykres funkcji o dany wektor
- graficznie rozwiązać układ nierówności liniowych z wartością bezwzględną
- interpretować treść zadania, sprawdzać zgodność otrzymanych wyników z warunkami zadania
- układać treść zadania do danego układu równań liniowych z dwiema niewiadomymi
- określać dziedzinę funkcji wymiernej
- wyznaczać miejsca zerowe funkcji stopnia drugiego
- rozwiązywać równania i nierówności liniowe ( o podwyższonym stopniu trudności) i oraz zadania tekstowe prowadzące do równań liniowych, np.:
- Pitagoras powiedział: :” Połowa moich uczniów studiuje matematykę, czwarta
część muzykę, siódma część milczy i oprócz tego są tam jeszcze 3 kobiety.” Ilu
uczniów było w szkole Pitagorasa?
- stosować zdobytą wiedzę dotyczącą równań liniowych do matematyzowania problemów z życia codziennego, np.;
- Do zbiornika prowadzą dwie rury. Jeżeli pierwsza rura będzie otwarta przez 5 minut, a druga przez 8 minut, to do zbiornika wpłynie 340 litrów wody. Jeżeli zaś pierwsza rura będzie otwarta przez 8 minut, a druga przez 5 minut, to wpłynie do zbiornika 310 litrów wody. Ile litrów wody wpływa przez pierwszą, a ile przez drugą w ciągu jednej minuty? |
Stopień |
Wymagania |
Dopuszczający (2)
|
Uczeń potrafi:
- narysować prostą przechodzącą przez dane punkty
- wskazać punkty należące i punkty nienależące do figury
- klasyfikować trójkąty ze względu na boki i kąty
- zaznaczać wysokości w trójkącie
- rozpoznawać czworokąty i je nazywać
- podawać twierdzenia o sumie miar kątów w trójkącie
- wymienić podstawowe jednostki długości i pola
- obliczać obwody i pola trójkątów, prostokątów, gdy dane są długości boków
- obliczać pola i obwody kół, gdy dany jest promień
- wskazywać i nazywać wielkości związane z okręgiem
- odróżniać koło od okręgu
- zapisywać formułę twierdzenia Pitagorasa
- znajdować długości przeciwprostokątnej gdy dane są długości przyprostokątnych
- wskazywać kąt środkowy i kąt wpisany w okręgu
- wskazywać zależności między kątem wpisanym i kątem środkowym opartych na tym samym łuku oraz kątami wpisanymi opartymi na tym samym łuku
- rysować poznana trójkąty i czworokąty
- odróżniać , czy dany wielokąt jest wpisany czy opisany na okręgu
- określać wzajemne położenie okręgów na płaszczyźnie
- narysować za pomocą linijki styczną i sieczną do okręgu
- narysować symetralną odcinka
- sporządzać rysunek w żądanej skali
|
Dostateczny (3)
|
Uczeń potrafi:
- stosować twierdzenie o sumie miar kątów w trójkącie
- rozpoznawać wielokąty i nazywać je
- przeliczać jednostki długości
- obliczać miary kata wpisanego ( środkowego), gdy dana jest miara kata wpisanego (środkowego)
- obliczać długości przekątnych w prostokącie i kwadracie
- obliczać długości wysokości w trójkącie równobocznym i równoramiennym
- obliczać pola i obwody prostokątów, korzystając z zależności podanych w zadaniu
- obliczać pola i obwody trójkątów
- obliczać promień koła, gdy dane jest jego pole lub obwód
- narysować symetralna odcinka i dwusieczną kąta
- konstrukcyjnie wpisać i opisać okrąg na trójkącie i kwadracie
- zapisywać proporcje wynikające z twierdzenia Talesa
- dzielić odcinek na równe części
- określać funkcje trygonometryczne kąta ostrego w trójkącie prostokątnym
- określać odległość rzeczywistą na podstawie planu i skali
|
Dobry (4)
|
Uczeń potrafi:
- podawać własności czworokątów i stosować je w zadaniach, np.:
-Pole rombu o wysokości 7 jest równe 84. Oblicz obwód tego rombu.
- obliczać pola i obwody wielokątów
- obliczać pole koła, gdy dany jest obwód i odwrotnie
- przeliczać jednostki pola
- konstrukcyjnie wpisać i opisać okrąg na czworokącie
- stosować twierdzenia Pitagorasa do rozwiązywania problemów praktycznych
- rozwiązywać trójkąty prostokątne
- stosować twierdzenie Talesa do rozwiązywania zadań
- podać wymiary na planie (mapie) znając skalę i rzeczywiste wymiary
- stosować funkcje trygonometryczne do rozwiązywania zadań o średnim stopniu trudności
- stosować zdobytą wiedzę do rozwiązywania typowych problemów z życia codziennego, np..:
-Ile należy zapłacić za drewniany płotek potrzebny do ogrodzenia klombu w kształcie koła o średnicy 15 cm, jeżeli metr bieżący tego płotka kosztuje 12,50 zł? Ile zwojów należy kupić, jeżeli w jednym są 3 metry bieżące płotka? |
Bardzo dobry (5) |
Uczeń potrafi:
- stosować własności wielokątów oraz zależności miedzy nimi
- konstruować wielokąty foremne
- stosować funkcje trygonometryczne do rozwiązywania zadań trudniejszych
- rozwiązywać trudniejsze zadania dotyczące czworokątów, np.:
- Oblicz pole trapezu ograniczonego osiami układu oraz prostymi o równaniach y = 6 i y = -3x + 9
- obliczać pola i obwody figur podobnych znając skalę podobieństwa i odwrotnie
- określać odległość rzeczywistą oraz w terenie na podstawie planu i skali
- ustalić skalę planu (mapy) znając wymiary rzeczywiste i na rysunku
- naszkicować plan obiektu w zadanej skali
- zastosować własności czworokąta wpisanego i opisanego na okręgu do rozwiązywania zadań
- obliczać pole i obwód koła oraz jego wycinka
- zastosować własności symetralnej odcinka i dwusiecznej kąta do rozwiązywania problemów
- stosować zdobytą wiedzę do rozwiązywania nietypowych problemów z życia codziennego
|
