Propozycja przedmiotowego systemu oceniania z matematyki do klasy II
wraz z określeniem wymagań edukacyjnych
(zakres rozszerzony)
Proponujemy, by omawiając dane zagadnienie programowe lub rozwiązując zadanie, nauczyciel określał do jakiego zakresu wiedzy je zalicza. Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i wykraczające poza program nauczania (W). Wymienione poziomy wymagań odpowiadają w przybliżeniu ocenom szkolnym. Nauczyciel, określając te poziomy, powinien zatem sprecyzować, czy opanowania pewnych czynności lub wiedzy będzie wymagał na ocenę dopuszczającą (2), dostateczną (3), dobrą (4), bardzo dobrą (5) lub celującą (6).
- Wymagania konieczne (K) dotyczą zagadnień elementarnych, stanowiących swego rodzaju podstawę, zatem powinny być opanowane przez każdego ucznia.
- Wymagania podstawowe (P) zawierają wymagania z poziomu (K), wzbogacone o typowe problemy o niewielkim stopniu trudności.
- Wymagania rozszerzające (R), zawierające wymagania z poziomów (K) i (P), dotyczą zagadnień bardziej złożonych i nieco trudniejszych.
- Wymagania dopełniające (D), zawierające wymagania z poziomów (K), (P) i (R), dotyczą zagadnień problemowych, trudniejszych, wymagających umiejętności przetwarzania przyswojonych informacji.
- Wymagania wykraczające (W) dotyczą zagadnień trudnych, oryginalnych, wykraczających poza obowiązkowy program nauczania.
Poniżej przedstawiony został podział wymagań na poszczególne oceny szkolne:
ocena dopuszczająca – wymagania na poziomie (K),
ocena dostateczna – wymagania na poziomie (K) i (P),
ocena dobra – wymagania na poziomie (K), (P) i (R),
ocena bardzo dobra – wymagania na poziomie (K), (P), (R) i (D),
ocena celująca – wymagania na poziomie (K), (P), (R), (D) i (W).
Oczywiście podział ten należy traktować jedynie jako propozycję. Poniżej przedstawiamy wymagania dla zakresu rozszerzonego. Połączenie wymagań koniecznych i podstawowych, a także rozszerzających i dopełniających, pozwoli nauczycielowi dostosować wymagania do specyfiki klasy.
1. WIELOMIANY
Poziom (K) lub (P)
Uczeń otrzymuje ocenę dopuszczającą lub dostateczną, jeśli:
-
podaje przykłady wielomianów, określa ich stopień i podaje wartości ich współczynników
|
-
zapisuje wielomian w sposób uporządkowany
|
-
oblicza wartość wielomianu dla danego argumentu; sprawdza, czy dany punkt należy do wykresu danego wielomianu
|
-
wyznacza sumę, różnicę, iloczyn wielomianów i określa ich stopień
|
-
szkicuje wykres wielomianu będącego sumą jednomianów stopnia pierwszego i drugiego
|
-
określa stopień iloczynu wielomianów bez wykonywania mnożenia
|
-
podaje współczynnik przy najwyższej potędze oraz wyraz wolny iloczynu wielomianów, bez wykonywania mnożenia wielomianów
|
-
oblicza wartość wielomianu dwóch (trzech) zmiennych dla danych argumentów
|
-
stosuje wzory na kwadrat i sześcian sumy i różnicy oraz wzór na różnicę kwadratów do wykonywania działań na wielomianach oraz do rozkładu wielomianu na czynniki
|
-
stosuje wzory na sumę i różnicę sześcianów
|
-
rozkłada wielomian na czynniki, stosując metodę grupowania wyrazów i wyłączania wspólnego czynnika poza nawias
|
-
dzieli wielomian przez dwumian 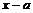
|
-
sprawdza poprawność wykonanego dzielenia
|
-
zapisuje wielomian w postaci 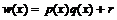
|
-
bez wykonywania dzielenia sprawdza podzielność wielomianu przez dwumian 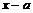
|
-
określa, które liczby mogą być pierwiastkami całkowitymi lub wymiernymi wielomianu
|
-
mając dany wielomian w postaci iloczynowej, wyznacza jego pierwiastki i podaje ich krotność
|
-
znając stopień wielomianu i jego pierwiastek, bada, czy wielomian ma inne pierwiastki oraz określa ich krotność
|
-
rozwiązuje proste równania wielomianowe
|
-
szkicuje wykres wielomianu, mając daną jego postać iloczynową
|
-
dobiera wzór wielomianu, mając dany szkic wykresu
|
-
rozwiązuje proste nierówności wielomianowe
|
-
opisuje wielomianem zależności dane w zadaniu i wyznacza jego dziedzinę
|
Poziom (R) lub (D)
Uczeń otrzymuje ocenę dobrą lub bardzo dobrą, jeśli opanował poziomy (K) i (P) oraz dodatkowo:
-
wyznacza współczynniki wielomianu, mając dane warunki
|
-
stosuje wielomiany wielu zmiennych w zadaniach różnych typów
|
-
stosuje wzór :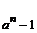
|
-
rozkłada wielomian na czynniki możliwie najniższego stopnia
|
-
stosuje rozkład wielomianu na czynniki w zadaniach różnych typów
|
-
analizuje i stosuje metodę podaną w przykładzie, aby rozłożyć dany wielomian na czynniki
|
-
bez wykonywania dzielenia sprawdza podzielność wielomianu przez wielomian 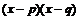
|
-
wyznacza iloraz danych wielomianów
|
-
wyznacza resztę z dzielenia wielomianu, mając zadane warunki
|
|
-
rozwiązuje zadania z parametrem dotyczące pierwiastków wielokrotnych
|
-
rozwiązuje równania i nierówności wielomianowe
|
-
stosuje nierówności wielomianowe do wyznaczenia dziedziny funkcji zapisanej za pomocą pierwiastka
|
-
rozwiązuje zadania z parametrem wymagające zastosowania twierdzenia Bézouta
|
-
opisuje za pomocą wielomianu objętość lub pole powierzchni bryły oraz określa dziedzinę powstałej w ten sposób funkcji
|
Poziom (W)
Uczeń otrzymuje ocenę celującą, jeśli opanował wiedzę i umiejętności z poziomów (K) – (D) oraz:
-
rozwiązuje zadania z parametrem, o podwyższonym stopniu trudności, dotyczące wyznaczania reszty z dzielenia wielomianu przez np. wielomian stopnia drugiego
|
-
stosuje równania i nierówności wielomianowe do rozwiązywania zadań praktycznych
|
-
przeprowadza dowody twierdzeń dotyczących wielomianów, np. twierdzenia Bézouta, twierdzenia o pierwiastkach całkowitych wielomianów
|
2. FUNKCJE WYMIERNE
Poziom (K) lub (P)
Uczeń otrzymuje ocenę dopuszczającą lub dostateczną, jeśli:
-
wskazuje wielkości odwrotnie proporcjonalne i stosuje taką zależność do rozwiązywania prostych zadań
|
-
szkicuje wykres funkcji 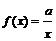 , gdzie , gdzie 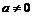 i podaje jej własności (dziedzinę, zbiór wartości, przedziały monotoniczności) i podaje jej własności (dziedzinę, zbiór wartości, przedziały monotoniczności)
|
-
szkicuje wykres funkcji 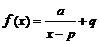 i podaje jej własności i podaje jej własności
|
-
wyznacza asymptoty wykresu powyższej funkcji
|
-
dobiera wzór funkcji do jej wykresu
|
-
przekształca wzór funkcji homograficznej do postaci kanonicznej w prostych przypadkach
|
-
wyznacza dziedzinę prostego wyrażenia wymiernego
|
-
oblicza wartość wyrażenia wymiernego dla danej wartości zmiennej
|
-
skraca i rozszerza wyrażenia wymierne
|
-
wykonuje działania na wyrażeniach wymiernych w prostych przypadkach i podaje odpowiednie założenia
|
-
rozwiązuje proste równania wymierne
|
-
rozwiązuje, również graficznie, proste nierówności wymierne
|
-
wykorzystuje wyrażenia wymierne do rozwiązywania prostych zadań tekstowych
|
-
wyznacza ze wzoru dziedzinę i miejsce zerowe funkcji wymiernej
|
-
stosuje własności wartości bezwzględnej do rozwiązywania prostych równań i nierówności wymiernych
|
Poziom (R) lub (D)
Uczeń otrzymuje ocenę dobrą lub bardzo dobrą, jeśli opanował poziomy (K) i (P) oraz dodatkowo:
-
rozwiązuje zadania tekstowe, stosując proporcjonalność odwrotną
|
-
przekształca wzór funkcji homograficznej do postaci kanonicznej
|
-
szkicuje wykresy funkcji homograficznych i określa ich własności
|
-
wyznacza wzór funkcji homograficznej spełniającej podane warunki
|
-
rozwiązuje zadania z parametrem dotyczące funkcji homograficznej
|
-
szkicuje wykresy funkcji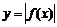 , , 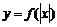 , , 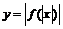 , gdzie , gdzie 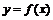 jest funkcją homograficzną i opisuje ich własności jest funkcją homograficzną i opisuje ich własności
|
-
wykonuje działania na wyrażeniach wymiernych i podaje odpowiednie założenia
|
-
przekształca wzory, stosując działania na wyrażeniach wymiernych
|
-
rozwiązuje równania i nierówności wymierne
|
-
rozwiązuje układy nierówności wymiernych
|
-
wykorzystuje wyrażenia wymierne do rozwiązywania trudniejszych zadań tekstowych
|
-
rozwiązuje zadania z parametrem dotyczące funkcji wymiernej
|
-
stosuje własności wartości bezwzględnej do rozwiązywania równań i nierówności wymiernych
|
-
zaznacza w układzie współrzędnych zbiory punktów spełniających zadane warunki
|
Poziom (W)
Uczeń otrzymuje ocenę celującą, jeśli opanował wiedzę i umiejętności z poziomów (K) – (D) oraz:
-
stosuje własności hiperboli do rozwiązywania zadań
|
-
stosuje funkcje wymierne do rozwiązywania zadań z parametrem o podwyższonym stopniu trudności
|
3. FUNKCJE TRYGONOMETRYCZNE
Poziom (K) lub (P)
Uczeń otrzymuje ocenę dopuszczającą lub dostateczną, jeśli:
-
rysuje w układzie współrzędnych kąt, wskazuje jego ramię początkowe i końcowe
|
-
wyznacza wartości funkcji trygonometrycznych kąta, gdy dane są współrzędne punktu leżącego na jego końcowym ramieniu
|
-
określa znaki funkcji trygonometrycznych danego kąta
|
-
korzystając z rysunku, oblicza wartości funkcji trygonometrycznych szczególnych kątów, np.: 90°, 120°, 135°, 225°
|
-
określa, w której ćwiartce układu współrzędnych leży końcowe ramię kąta, mając dane wartości funkcji trygonometrycznych
|
-
zamienia miarę stopniową na łukową i odwrotnie
|
-
odczytuje okres podstawowy funkcji na podstawie jej wykresu
|
-
szkicuje wykresy funkcji trygonometrycznych w danym przedziale i określa ich własności
|
-
szkicuje wykresy funkcji trygonometrycznych, stosując przesunięcie o wektor i określa ich własności
|
-
szkicuje wykresy funkcji trygonometrycznych, stosując symetrię względem osi układu współrzędnych oraz symetrię względem początku układu współrzędnych i określa ich własności
|
-
szkicuje wykresy funkcji 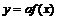 oraz oraz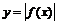 , gdzie , gdzie 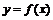 jest funkcją trygonometryczną i określa ich własności jest funkcją trygonometryczną i określa ich własności
|
-
stosuje tożsamości trygonometryczne w prostych sytuacjach
|
-
dowodzi proste tożsamości trygonometryczne, podając odpowiednie założenia
|
-
oblicza wartości pozostałych funkcji trygonometrycznych, znając wartość funkcji sinus lub cosinus
|
-
wyznacza wartości funkcji trygonometrycznych kątów z zastosowaniem wzorów na funkcje trygonometryczne sumy i różnicy kątów
|
-
stosuje wzory na funkcje trygonometryczne kąta podwojonego w prostych przypadkach
|
-
wyznacza wartości funkcji trygonometrycznych danych kątów z zastosowaniem wzorów redukcyjnych
|
-
rozwiązuje proste równania i nierówności trygonometryczne
|
-
posługuje się tablicami lub kalkulatorem do wyznaczenia kąta, przy danej wartości funkcji trygonometrycznej
|
Poziom (R) lub (D)
Uczeń otrzymuje ocenę dobrą lub bardzo dobrą, jeśli opanował poziomy (K) i (P) oraz dodatkowo:
-
oblicza wartości funkcji trygonometrycznych szczególnych kątów, np.: – 90°, 315°, 1080°
|
-
stosuje funkcje trygonometryczne do rozwiązywania zadań
|
-
oblicza wartości funkcji trygonometrycznych dowolnych kątów
|
-
wyznacza kąt, mając daną wartość jednej z jego funkcji trygonometrycznych
|
-
szkicuje wykres funkcji okresowej
|
-
stosuje okresowość funkcji do wyznaczania jej wartości
|
-
wykorzystuje własności funkcji trygonometrycznych do obliczenia wartości tej funkcji dla danego kąta
|
-
szkicuje wykresy funkcji 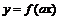 oraz oraz 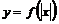 , gdzie , gdzie 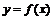 jest funkcją trygonometryczną i określa ich własności jest funkcją trygonometryczną i określa ich własności
|
-
szkicuje wykresy funkcji trygonometrycznych, stosując złożenia różnych przekształceń wykresu funkcji trygonometrycznej oraz określa ich własności
|
-
oblicza wartości pozostałych funkcji trygonometrycznych, znając wartość funkcji tangens lub cotangens
|
-
stosuje wzory na funkcje trygonometryczne podwojonego argumentu do przekształcania wyrażeń, w tym również do uzasadniania tożsamości trygonometrycznych
|
-
stosuje związki między funkcjami trygonometrycznymi do rozwiązywania trudniejszych równań i nierówności trygonometrycznych
|
Poziom (W)
Uczeń otrzymuje ocenę celującą, jeśli opanował wiedzę i umiejętności z poziomów (K) – (D) oraz:
-
wyprowadza wzory na funkcje trygonometryczne sumy i różnicy kątów oraz na funkcje kąta podwojonego
|
-
rozwiązuje zadania o znacznym stopniu trudności dotyczące funkcji trygonometrycznych
|
4. FUNKCJE WYKŁADNICZE I LOGARYTMICZNE
Poziom (K) lub (P)
Uczeń otrzymuje ocenę dopuszczającą lub dostateczną, jeśli:
-
oblicza pierwiastek n-tego stopnia z liczby nieujemnej
|
-
oblicza potęgi o wykładnikach wymiernych
|
-
zapisuje daną liczbę w postaci potęgi o wykładniku wymiernym
|
-
zapisuje daną liczbę w postaci potęgi o danej podstawie
|
-
upraszcza wyrażenia, stosując prawa działań na potęgach w prostych przypadkach
|
-
porównuje liczby, korzystając z własności funkcji wykładniczej
|
-
wyznacza wzór funkcji wykładniczej lub logarytmicznej i szkicuje jej wykres, znając współrzędne punktu należącego do jej wykresu
|
-
szkicuje wykres funkcji wykładniczej i logarytmicznej, stosując przesunięcie o wektor i określa jej własności
|
-
szkicuje wykres funkcji, będący efektem jednego przekształcenia wykresu funkcji wykładniczej lub logarytmicznej i określa jej własności
|
-
rozwiązuje proste równania wykładnicze i logarytmiczne, korzystając z różnowartościowości funkcji wykładniczej
|
-
rozwiązuje proste nierówności wykładnicze i logarytmiczne, korzystając z monotoniczności funkcji wykładniczej
|
-
oblicza logarytm danej liczby
|
-
stosuje równości wynikające z definicji logarytmu do prostych obliczeń
|
-
stosuje twierdzenia o logarytmach do obliczania wartości wyrażeń z logarytmami
|
-
zamienia podstawę danego logarytmu na inną, wskazaną
|
Poziom (R) lub (D)
Uczeń otrzymuje ocenę dobrą lub bardzo dobrą, jeśli opanował poziomy (K) i (P) oraz dodatkowo:
-
upraszcza wyrażenia, stosując prawa działań na potęgach
|
-
porównuje liczby przedstawione w postaci potęg
|
-
szkicuje wykresy funkcji wykładniczej lub logarytmicznej otrzymane w wyniku złożenia kilku przekształceń
|
-
rozwiązuje równania wykładnicze i logarytmiczne, korzystając z różnowartościowości funkcji wykładniczej
|
-
rozwiązuje nierówności wykładnicze i logarytmiczne, korzystając z monotoniczności funkcji wykładniczej
|
-
wykorzystuje własności funkcji wykładniczej i logarytmicznej do rozwiązywania zadań o kontekście praktycznym
|
-
stosuje wykresy funkcji logarytmicznych do rozwiązywania zadań, w tym również do ustalenia liczby rozwiązań równania w zależności od parametru
|
Poziom (W)
Uczeń otrzymuje ocenę celującą, jeśli opanował wiedzę i umiejętności z poziomów (K) – (D) oraz:
-
dowodzi twierdzenia o logarytmach
|
-
wykorzystuje twierdzenie o zmianie podstawy logarytmu w zadaniach na dowodzenie
|
-
rozwiązuje zadania o znacznym stopniu trudności dotyczące funkcji wykładniczej i logarytmicznej
|
5. CIĄGI
Poziom (K) lub (P)
Uczeń otrzymuje ocenę dopuszczającą lub dostateczną, jeśli:
-
wyznacza kolejne wyrazy ciągu, gdy danych jest kilka jego początkowych wyrazów
|
|
-
wyznacza wzór ogólny ciągu, mając danych kilka jego początkowych wyrazów
|
-
wyznacza początkowe wyrazy ciągu określonego wzorem ogólnym oraz ciągu określonego rekurencyjnie
|
-
wyznacza, które wyrazy ciągu przyjmują daną wartość
|
-
podaje przykłady ciągów monotonicznych, których wyrazy spełniają dane warunki
|
-
mając dane kolejne wyrazy ciągu, uzasadnia, że dany ciąg nie jest monotoniczny
|
-
wyznacza wyraz 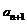 ciągu określonego wzorem ogólnym ciągu określonego wzorem ogólnym
|
-
wyznacza wzór ogólny ciągu będącego wynikiem wykonania działań na danych ciągach w prostych przypadkach
|
-
podaje przykłady ciągów arytmetycznych
|
-
wyznacza wyrazy ciągu arytmetycznego, mając dany pierwszy wyraz i różnicę
|
-
wyznacza wzór ogólny ciągu arytmetycznego, mając dane dowolne dwa jego wyrazy
|
-
sprawdza w prostych przypadkach, czy dany ciąg jest arytmetyczny
|
-
oblicza sumę n początkowych wyrazów ciągu arytmetycznego
|
-
podaje przykłady ciągów geometrycznych
|
-
wyznacza wyrazy ciągu geometrycznego, mając dany pierwszy wyraz i iloraz
|
-
wyznacza wzór ogólny ciągu geometrycznego, mając dane dowolne dwa jego wyrazy
|
-
sprawdza, w prostych przypadkach, czy dany ciąg jest geometryczny
|
-
oblicza sumę n początkowych wyrazów ciągu geometrycznego
|
-
oblicza wysokość kapitału przy różnym okresie kapitalizacji
|
-
oblicza oprocentowanie lokaty w prostych sytuacjach
|
Poziom (R) lub (D)
Uczeń otrzymuje ocenę dobrą lub bardzo dobrą, jeśli opanował poziomy (K) i (P) oraz dodatkowo:
-
wyznacza wzór ogólny ciągu spełniającego podane warunki
|
-
bada monotoniczność ciągów
|
-
rozwiązuje zadania o podwyższonym stopniu trudności związane ze wzorem rekurencyjnym ciągu
|
-
rozwiązuje zadania z parametrem dotyczące monotoniczności ciągu
|
-
sprawdza w trudniejszych przypadkach, czy dany ciąg jest arytmetyczny
|
-
sprawdza w trudniejszych przypadkach, czy dany ciąg jest geometryczny
|
-
rozwiązuje równania z zastosowaniem wzoru na sumę wyrazów ciągu arytmetycznego i geometrycznego
|
-
określa monotoniczność ciągu arytmetycznego i geometrycznego
|
-
rozwiązuje zadania związane z kredytami dotyczące okresu oszczędzania i wysokości oprocentowania w trudniejszych przypadkach
|
-
stosuje własności ciągu arytmetycznego i geometrycznego w zadaniach
|
Poziom (W)
Uczeń otrzymuje ocenę celującą, jeśli opanował wiedzę i umiejętności z poziomów (K) – (D) oraz:
-
rozwiązuje zadania o podwyższonym stopniu trudności dotyczące monotoniczności ciągu
|
-
stosuje średnią geometryczną do rozwiązywania zadań
|
-
rozwiązuje zadania o znacznym stopniu trudności dotyczące ciągów
|
6. PLANIMETRIA
Poziom (K) lub (P)
Uczeń otrzymuje ocenę dopuszczającą lub dostateczną, jeśli:
-
określa wzajemne położenie okręgów, mając dane promienie tych okręgów oraz odległość ich środków
|
-
określa, ile punktów wspólnych mają prosta i okrąg przy danych warunkach
|
-
stosuje własności stycznej do okręgu do rozwiązywania prostych zadań
|
-
rozpoznaje kąty wpisane i środkowe w okręgu oraz wskazuje łuki, na których są one oparte
|
-
stosuje, w prostych przypadkach, twierdzenie o kącie środkowym i wpisanym, opartych na tym samym łuku oraz twierdzenie o kącie między styczną a cięciwą okręgu
|
-
stosuje twierdzenia o cięciwach, siecznych, stycznej i siecznej do rozwiązywania zadań w prostych sytuacjach
|
-
rozwiązuje zadania dotyczące okręgu wpisanego w trójkąt prostokątny lub równoramienny
|
-
rozwiązuje zadania związane z okręgiem opisanym na trójkącie prostokątnym lub równoramiennym
|
-
określa własności czworokątów i stosuje je do rozwiązywania prostych zadań
|
-
sprawdza, czy w dany czworokąt można wpisać okrąg
|
-
sprawdza, czy na danym czworokącie można opisać okrąg
|
-
stosuje twierdzenie sinusów do wyznaczenia długości boku trójkąta, miary kąta lub długości promienia okręgu opisanego na trójkącie
|
-
stosuje twierdzenie cosinusów do wyznaczenia długości boku lub miary kąta trójkąta
|
-
oblicza odległość punktów w układzie współrzędnych
|
-
wyznacza współrzędne środka odcinka, mając dane współrzędne jego końców
|
-
oblicza odległość punktu od prostej
|
-
oblicza odległość między prostymi równoległymi
|
-
wyznacza środek i promień okręgu, mając jego równanie
|
-
opisuje równaniem okrąg o danym środku i przechodzący przez dany punkt
|
-
rozwiązuje algebraicznie i graficznie układy równań, z których jedno jest pierwszego, a drugie drugiego stopnia
|
-
opisuje koło w układzie współrzędnych
|
-
sprawdza, czy punkt należy do danego okręgu (koła)
|
-
podaje, w prostych przypadkach, geometryczną interpretację rozwiązania układu nierówności stopnia drugiego
|
-
sprawdza, czy wektory mają ten sam kierunek i zwrot
|
-
wykonuje działania na wektorach
|
-
stosuje działania na wektorach do badania współliniowości punktów
|
-
stosuje działania na wektorach do podziału odcinka
|
-
konstruuje figury jednokładne
|
-
wyznacza współrzędne punktów w danej jednokładności
|
Poziom (R) lub (D)
Uczeń otrzymuje ocenę dobrą lub bardzo dobrą, jeśli opanował poziomy (K) i (P) oraz dodatkowo:
-
stosuje własności stycznej do okręgu do rozwiązywania trudniejszych zadań
|
-
stosuje twierdzenie o kącie środkowym i wpisanym, opartych na tym samym łuku oraz twierdzenie o kącie między styczną a cięciwą okręgu do rozwiązywania zadań o większym stopniu trudności
|
-
stosuje twierdzenia o cięciwach, siecznych, stycznej i siecznej do rozwiązywania trudniejszych zadań
|
-
rozwiązuje zadania związane z okręgiem wpisanym w dowolny trójkąt i opisanym na dowolnym trójkącie
|
-
rozwiązuje zadania dotyczące okręgu wpisanego w czworokąt i okręgu opisanego na czworokącie
|
-
stosuje różne wzory na pole trójkąta
|
-
stosuje własności środka okręgu opisanego na trójkącie w zadaniach z geometrii analitycznej
|
-
stosuje własności czworokątów wypukłych do rozwiązywania trudniejszych zadań z planimetrii
|
-
stosuje twierdzenie sinusów do rozwiązywania trójkątów
|
-
stosuje twierdzenie cosinusów do rozwiązywania trójkątów
|
-
stosuje wzór na odległość między punktami do rozwiązywania zadań dotyczących równoległoboków
|
-
stosuje związek między współczynnikiem kierunkowym a kątem nachylenia prostej do osi OX
|
-
wyznacza kąt między prostymi
|
-
sprawdza, czy dane równanie jest równaniem okręgu
|
-
wyznacza wartość parametru tak, aby równanie opisywało okrąg
|
-
stosuje równanie okręgu w zadaniach
|
-
stosuje układy równań drugiego stopnia do rozwiązywania zadań z geometrii analitycznej
|
-
opisuje układem nierówności przedstawiony podzbiór płaszczyzny
|
-
zaznacza w układzie współrzędnych zbiory spełniające określone warunki
|
-
stosuje działania na wektorach oraz ich interpretację geometryczną w zadaniach
|
-
stosuje własności jednokładności w zadaniach
|
Poziom (W)
Uczeń otrzymuje ocenę celującą, jeśli opanował wiedzę i umiejętności z poziomów (K) – (D) oraz:
-
dowodzi twierdzenia dotyczące okręgu wpisanego w czworokąt i okręgu opisanego na czworokącie
|
-
przeprowadza dowód twierdzenia sinusów i twierdzenia cosinusów
|
-
wyprowadza wzór na odległość punktu od prostej
|
-
wykorzystuje działania na wektorach do dowodzenia twierdzeń
|
-
rozwiązuje zadania z planimetrii o znacznym stopniu trudności
|
-
dowodzi twierdzenia o cięciwach, siecznych, stycznej i siecznej
|
Wykaz zakładanych osiągnięć ucznia klasy II liceum
– zakres rozszerzony
W zakresie wielomianów uczeń:
- posługuje się wzorami skróconego mnożenia:
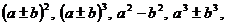
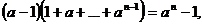
- rozkłada wielomiany na czynniki, stosując wzory skróconego mnożenia, grupowanie wyrazów, wyłączanie wspólnego czynnika poza nawias,
- dodaje, odejmuje i mnoży wielomiany,
- wykonuje dzielenie wielomianu przez dwumian
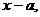
- stosuje twierdzenie o reszcie z dzielenia wielomianu przez dwumian
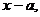
- stosuje twierdzenie o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych,
- rozwiązuje równania i nierówności wielomianowe,
- stosuje wielomiany w kontekście praktycznym.
W zakresie funkcji wymiernych uczeń:
- sporządza wykres, odczytuje własności i rozwiązuje zadania umieszczone w kontekście praktycznym, związane z proporcjonalnością odwrotną,
- wyznacza dziedzinę wyrażenia wymiernego z jedną zmienną oraz oblicza jego wartość liczbową dla danej wartości zmiennej,
- dodaje, odejmuje, mnoży i dzieli wyrażenia wymierne,
- skraca i rozszerza wyrażenia wymierne,
- sporządza wykres oraz podaje własności funkcji homograficznej,
- rozwiązuje proste równania wymierne, np.:
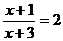 ;
; 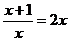 ,
,
- rozwiązuje proste nierówności wymierne, np.:
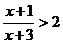 ;
; 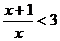 ,
,
- rozwiązuje zadania umieszczone w kontekście praktycznym, prowadzące do rozwiązywania prostych równań wymiernych.
W zakresie funkcji trygonometrycznych uczeń:
- stosuje miarę łukową i miarę stopniową kąta,
- wykorzystuje definicje i wyznacza wartości funkcji trygonometrycznych dla kątów ostrych,
- wyznacza wartości funkcji trygonometrycznych dowolnego kąta przez sprowadzenie do przypadku kąta ostrego,
- znając wartość jednej z funkcji trygonometrycznych, wyznacza wartości pozostałych funkcji tego samego kąta ostrego,
- stosuje związki: sin2a + cos2a = 1,
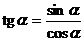 oraz wzory na sinus i cosinus sumy i różnicy kątów w dowodach tożsamości trygonometrycznych,
oraz wzory na sinus i cosinus sumy i różnicy kątów w dowodach tożsamości trygonometrycznych,
- rozwiązuje proste równania trygonometryczne typu:
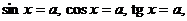
- posługuje się wykresami funkcji trygonometrycznych przy rozwiązywaniu nierówności typu
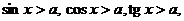
- szkicuje, na podstawie wykresu funkcji trygonometrycznej y = f(x), wykresy funkcji: y = cf (x), y = f(dx) oraz wykresy będące efektem wykonania kilku operacji,
- rozwiązuje równania i nierówności trygonometryczne, na przykład:
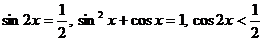 .
.
W zakresie funkcji wykładniczych i logarytmicznych uczeń:
- oblicza potęgi o wykładnikach wymiernych oraz stosuje prawa działań na potęgach o wykładnikach wymiernych i rzeczywistych,
- zna definicję logarytmu i stosuje w obliczeniach wzory na logarytm iloczynu, logarytm ilorazu i logarytm potęgi oraz wzór na zamianę podstawy logarytmu,
- sporządza wykresy funkcji wykładniczych i logarytmicznych dla różnych podstaw,
- rozwiązuje zadania umieszczone w kontekście praktycznym z wykorzystaniem funkcji wykładniczej i logarytmicznej.
W zakresie ciągów liczbowych uczeń:
- wyznacza wyrazy ciągu określonego wzorem ogólnym lub rekurencyjnym,
- bada, czy dany ciąg jest arytmetyczny lub geometryczny,
- stosuje wzór na n-ty wyraz oraz sumę n początkowych wyrazów ciągu arytmetycznego i ciągu geometrycznego, również umieszczone w kontekście praktycznym.
W zakresie planimetrii uczeń:
- korzysta ze związków między kątem środkowym, kątem wpisanym i kątem między styczną a cięciwą okręgu,
- stosuje twierdzenie o związkach miarowych między odcinkami stycznych i siecznych,
- stosuje twierdzenia charakteryzujące czworokąty wpisane w okrąg i czworokąty opisane na okręgu,
- znajduje związki miarowe w figurach płaskich, w tym z zastosowaniem trygonometrii, również w zadaniach umieszczonych w kontekście praktycznym,
- znajduje związki miarowe w figurach płaskich z zastosowaniem twierdzenia sinusów i twierdzenia cosinusów,
- stosuje własności figur podobnych i jednokładnych w zadaniach, także umieszczonych w kontekście praktycznym,
- określa wzajemne położenie prostej i okręgu,
- rozwiązuje zadania dotyczące wzajemnego położenia prostej i okręgu oraz dwóch okręgów na płaszczyźnie kartezjańskiej,
- oblicza odległości punktów oraz odległość punktu od prostej na płaszczyźnie kartezjańskiej,
- wyznacza współrzędne środka odcinka,
- posługuje się równaniem okręgu
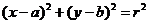 ; rozwiązuje układy równań, prowadzące do równań kwadratowych,
; rozwiązuje układy równań, prowadzące do równań kwadratowych,
- opisuje koło za pomocą nierówności,
- oblicza współrzędne oraz długość wektora, dodaje i odejmuje wektory oraz mnoży je przez liczbę,
- interpretuje geometrycznie działania na wektorach,
- stosuje wektory do rozwiązywania zadań, a także do dowodzenia własności figur,
- stosuje wektory do opisu przesunięcia wykresu funkcji.
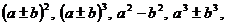
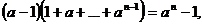
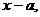
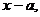
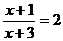 ;
; 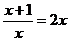 ,
,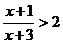 ;
; 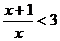 ,
,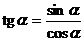 oraz wzory na sinus i cosinus sumy i różnicy kątów w dowodach tożsamości trygonometrycznych,
oraz wzory na sinus i cosinus sumy i różnicy kątów w dowodach tożsamości trygonometrycznych,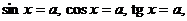
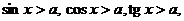
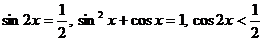 .
.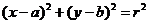 ; rozwiązuje układy równań, prowadzące do równań kwadratowych,
; rozwiązuje układy równań, prowadzące do równań kwadratowych,