Przedmiotowy system oceniania z matematyki
wraz z określeniem wymagań edukacyjnych
(zakres podstawowy i rozszerzony)
Klasa 1 LO
Proponujemy, by omawiając dane zagadnienie programowe lub rozwiązując zadanie, nauczyciel określał, do jakiego zakresu wiedzy je zalicza. Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i wykraczające poza program nauczania (W). Wymienione poziomy wymagań odpowiadają
w przybliżeniu ocenom szkolnym. Nauczyciel, określając te poziomy, powinien zatem sprecyzować, czy opanowania pewnych czynności lub wiedzy będzie wymagał na ocenę dopuszczającą (2), dostateczną (3), dobrą (4), bardzo dobrą (5) lub celującą (6).
- Wymagania konieczne (K) dotyczą zagadnień elementarnych, stanowiących swego rodzaju podstawę, zatem powinny być opanowane przez każdego ucznia.
- Wymagania podstawowe (P) zawierają wymagania z poziomu (K), wzbogacone
o typowe problemy o niewielkim stopniu trudności. - Wymagania rozszerzające (R), zawierające wymagania z poziomów (K) i (P), dotyczą zagadnień bardziej złożonych i nieco trudniejszych.
- Wymagania dopełniające (D), zawierające wymagania z poziomów (K), (P) i (R), dotyczą zagadnień problemowych, trudniejszych, wymagających umiejętności przetwarzania przyswojonych informacji.
- Wymagania wykraczające (W) dotyczą zagadnień trudnych, oryginalnych, wykraczających poza obowiązkowy program nauczania.
Poniżej przedstawiony został podział wymagań na poszczególne oceny szkolne:
ocena dopuszczająca – wymagania na poziomie (K),
ocena dostateczna – wymagania na poziomie (K) i (P),
ocena dobra – wymagania na poziomie (K), (P) i (R),
ocena bardzo dobra – wymagania na poziomie (K), (P), (R) i (D),
ocena celująca – wymagania na poziomie (K), (P), (R), (D) i (W).
Oczywiście podział ten należy traktować jedynie jako propozycję. Poniżej przedstawiamy wymagania dla zakresu podstawowego oraz rozszerzonego. Połączenie wymagań koniecznych i podstawowych a także rozszerzających i dopełniających pozwoli nauczycielowi dostosować wymagania do specyfiki klasy.
Wszystkie umiejętności zapisane w tabeli zwykłą czcionką dotyczą zarówno kształcenia
w zakresie podstawowym, jak i rozszerzonym. Wymagania programowe dotyczące kształcenia w zakresie rozszerzonym zapisano pogrubioną czcionką.
1. LICZBY RZECZYWISTE
Poziom (K) lub (P)
Uczeń otrzymuje ocenę dopuszczającą lub dostateczną, jeśli:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Poziom (R) lub (D)
Uczeń otrzymuje ocenę dobrą lub bardzo dobrą, jeśli opanował poziomy (K) i (P) oraz dodatkowo:
|
|
|
|
|
|
|
|
|
|
|
|
Poziom (W)
Uczeń otrzymuje ocenę celującą, jeśli opanował wiedzę i umiejętności z poziomów (K) – (D) oraz:
|
|
|
|
|
2. JĘZYK MATEMATYKI
Poziom (K) lub (P)
Uczeń otrzymuje ocenę dopuszczającą lub dostateczną, jeśli:
|
|
|
|
|
|
|
|
|
|
|
Poziom (R) lub (D)
Uczeń otrzymuje ocenę dobrą lub bardzo dobrą, jeśli opanował poziomy (K) i (P) oraz dodatkowo:
|
|
|
|
|
Poziom (W)
Uczeń otrzymuje ocenę celującą, jeśli opanował wiedzę i umiejętności z poziomów (K) – (D) oraz:
|
|
|
|
3. FUNKCJE
Poziom (K) lub (P)
Uczeń otrzymuje ocenę dopuszczającą lub dostateczną, jeśli:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Poziom (R) lub (D)
Uczeń otrzymuje ocenę dobrą lub bardzo dobrą, jeśli opanował poziomy (K) i (P) oraz dodatkowo:
|
|
|
|
|
|
|
|
|
Poziom (W)
Uczeń otrzymuje ocenę celującą, jeśli opanował wiedzę i umiejętności z poziomów (K) – (D) oraz:
|
|
|
4. FUNKCJA LINIOWA
Poziom (K) lub (P)
Uczeń otrzymuje ocenę dopuszczającą lub dostateczną, jeśli:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Poziom (R) lub (D)
Uczeń otrzymuje ocenę dobrą lub bardzo dobrą, jeśli opanował poziomy (K) i (P) oraz dodatkowo:
|
|
|
|
|
|
|
|
|
Poziom (W)
Uczeń otrzymuje ocenę celującą, jeśli opanował wiedzę i umiejętności z poziomów (K) – (D) oraz:
|
|
|
|
|
5. FUNKCJA KWADRATOWA
Poziom (K) lub (P)
Uczeń otrzymuje ocenę dopuszczającą lub dostateczną, jeśli:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Poziom (R) lub (D)
Uczeń otrzymuje ocenę dobrą lub bardzo dobrą, jeśli opanował poziomy (K) i (P) oraz dodatkowo:
|
|
|
|
|
|
|
|
Poziom (W)
Uczeń otrzymuje ocenę celującą, jeśli opanował wiedzę i umiejętności z poziomów (K) – (D) oraz:
|
|
|
|
|
6. PLANIMETRIA
Poziom (K) lub (P)
Uczeń otrzymuje ocenę dopuszczającą lub dostateczną, jeśli:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
oblicza wartości pozostałych funkcji trygonometrycznych, mając dany sinus lub cosinus kąta |
|
|
|
|
|
|
Poziom (R) lub (D)
Uczeń otrzymuje ocenę dobrą lub bardzo dobrą, jeśli opanował poziomy (K) i (P) oraz dodatkowo:
|
|
|
|
|
|
|
|
Poziom (W)
Uczeń otrzymuje ocenę celującą, jeśli opanował wiedzę i umiejętności z poziomów (K) – (D) oraz:
|
|
|
|
|
|
|
Wykaz zakładanych osiągnięć ucznia klasy I liceum
(osiągnięcia ucznia w zakresie rozszerzonym przedstawiono pogrubioną czcionką)
W zakresie liczb rzeczywistych uczeń:
- podaje przykłady liczb: naturalnych, całkowitych, wymiernych, niewymiernych, pierwszych i złożonych oraz przyporządkowuje liczbę do odpowiedniego zbioru liczb,
- przedstawia liczbę naturalną w postaci iloczynu liczb pierwszych,
- porównuje liczby wymierne,
- przedstawia liczby wymierne w różnych postaciach (ułamek zwykły, dziesiętny),
- wykonuje obliczenia na liczbach wymiernych i rzeczywistych,
- wyznacza przybliżenia liczby rzeczywistej z zadaną dokładnością (również przy użyciu kalkulatora),
- wykonuje działania na potęgach o wykładnikach całkowitych,
- oblicza wartości pierwiastków, w tym również pierwiastków nieparzystego stopnia z liczb ujemnych,
- usuwa niewymierność z mianownika ułamka,
- szacuje wyniki obliczeń z zadaną dokładnością,
- posługuje się pojęciami procentu i punktu procentowego w rozwiązywaniu zadań praktycznych,
- wykonuje działania na wyrażeniach algebraicznych (w tym stosuje wzory skróconego mnożenia).
W zakresie języka matematyki uczeń:
- zapisuje przedział liczbowy i przedstawia go na osi liczbowej,
- zaznacza na osi liczbowej zbiory określone koniunkcją lub alternatywą równań oraz nierówności,
- wyznacza wartość bezwzględną liczby rzeczywistej oraz stosuje jej interpretację geometryczną,
- rozwiązuje proste równania i nierówności z wartością bezwzględną
(np.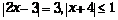 ),
), - wyznacza błąd bezwzględny oraz błąd względny przybliżenia liczby.
W zakresie funkcji uczeń:
- określa funkcję (wzorem, tabelką, wykresem, grafem, opisem słownym),
- na podstawie wykresu funkcji
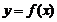 sporządza wykresy funkcji:
sporządza wykresy funkcji: 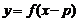 ,
, 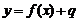 ,
,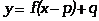 ,
,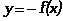 ,
,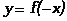 ,
, - na podstawie wykresu funkcji
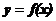 sporządza wykres funkcji
sporządza wykres funkcji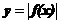 oraz wykresy będące efektem wykonania kilku operacji,
oraz wykresy będące efektem wykonania kilku operacji, - odczytuje z wykresu: dziedzinę funkcji, zbiór wartości funkcji, miejsca zerowe funkcji, przedziały monotoniczności funkcji, znaki wartości funkcji, wartość największą i najmniejszą funkcji,
- stosuje funkcje i ich własności w sytuacjach praktycznych.
W zakresie funkcji liniowej uczeń:
- sporządza wykresy funkcji liniowych,
- interpretuje współczynniki w równaniu kierunkowym prostej,
- wykorzystuje warunek równoległości i prostopadłości prostych do rozwiązywania zadań,
- rozwiązuje algebraicznie oraz interpretuje geometrycznie układy równań liniowych z dwiema niewiadomymi,
- interpretuje geometrycznie układy nierówności liniowych z dwiema niewiadomymi.
W zakresie funkcji kwadratowej uczeń:
- przedstawia wzór funkcji kwadratowej w różnych postaciach (ogólnej, iloczynowej, kanonicznej),
- sporządza wykresy funkcji kwadratowych,
- odczytuje własności funkcji kwadratowej z jej wykresu,
- wyznacza najmniejszą i największą wartość funkcji kwadratowej w przedziale domkniętym,
- wyznacza miejsca zerowe funkcji kwadratowej,
- rozwiązuje równania i nierówności kwadratowe z jedną niewiadomą,
- stosuje wzory Viete’a,
- rozwiązuje równania kwadratowe z parametrem,
- rozwiązuje nierówności kwadratowe z parametrem,
- wykorzystuje własności funkcji kwadratowej do rozwiązywania zadań praktycznych.
W zakresie planimetrii uczeń:
- wykorzystuje własności boków i kątów trójkątów,
- stosuje cechy przystawania i podobieństwa trójkątów,
- stosuje twierdzenie Talesa,
- wykorzystuje własności trójkątów prostokątnych,
- wyznacza wartości funkcji trygonometrycznych kąta ostrego oraz miarę kąta, gdy dana jest wartość funkcji trygonometrycznej tego kąta,
- znając wartość jednej z funkcji trygonometrycznych kąta ostrego, wyznacza wartości pozostałych funkcji,
- oblicza obwody i pola podstawowych figur płaskich, także z zastosowaniem trygonometrii.
